LAPW0 (generates potential) (from userguide)

lapw0 computes the total potential $V_{tot}$ as the sum of the Coulomb

and the exchange-correlation

potential 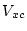$V_{xc}$ using the total electron (spin) density as input. It generates the spherical part (l=0) as case.vsp and the non-spherical part as case.vns. For spin-polarized systems, the spin-densities case.clmup and case.clmdn lead to two pairs of potential files. These files are called: case.vspup, case.vnsupand case.vspdn, case.vnsdn.

The Coulomb potential is calculated by the multipolar Fourier expansion introduced by Weinert (81). Utilizing the spatial partitioning of the unit cell and the dual representation of the charge density [equ. 2.10], firstly the multipole moments inside the spheres are calculated (Q-sp). The Fourier series of the charge density in the interstitial also represent SOME density inside the spheres, but certainly NOT the correct density there. Nevertheless, the multipole moments of this artificial plane-wave density inside each sphere are also calculated (Q-pw). By subtracting Q-pw from Q-sp one obtains pseudo-multipole moments Q. Next a new plane-wave series is generated which has two properties, namely zero density in the interstitial region and a charge distribution inside the spheres that reproduces the pseudo-multipole moments Q. This series is added to the original interstitial Fourier series for the density to form a new series which has two desirable properties: it simultaneously represents the interstitial charge density AND it has the same multipole moments inside the spheres as the actual density. Using this Fourier series the interstitial Coulomb potential follows immediately by dividing the Fourier coefficients by

(up to a constant).

Inside the spheres the Coulomb potential is obtained by a straightforward classical Green's function method for the solution of the boundary value problem.

The exchange-correlation potential is computed numerically on a grid. Inside the atomic spheres a least squares procedure is used to reproduce the potential using a lattice harmonics representation (the linear equations are solved with modified LINPACK routines). In the interstitial region a 3-dimensional fast Fourier transformation (FFT) is used.

The total potential

is obtained by summation of the Coulomb

and exchange-correlation potentials $V_{xc}$ .
In order to find the contribution from the plane wave representation to the Hamilton matrix elements we reanalyze the Fourier series in such a way that the new series represents a potential which is zero inside the spheres but keeps the original value in the interstitial region and this series is put into case.vns.

The contribution to the total energy which involves integrals of the form $\rho*V$ is calculated according to the formalism of Weinert et al (82).

The Hellmann-Feynman force contribution to the total force is also calculated (Yu et al 91).
Finally, the electric field gradient (EFG) is calculated in case you have an L=2 term in the density expansion. The EFG tensor is given in both, the ``local-rotation-matrix'' coordinate system, and then diagonalized. The resulting eigenvectors of this rotation are given by columns.

For surface calculations the total and electrostatic potential at z=0 and z=0.5 is calculated and can be used as energy-zero for the determination of the workfunction. (It is assumed that the middle of your vacuum region is either at z=0 or z=0.5).

Reference: http://euler.phys.cmu.edu/cluster/WIEN2k/7SCF_cycle.html