There are 4 parametrizations in the mBJ method.
First parametrization: Unmodified version of Beck-Johnson
Recently, Becke and Johnson15 (BJ) proposed an exchange potential, which was designed to reproduce the exact exchange potential in atoms. The BJ potential, which does not contain any empirical parameter, reads
The first contribution to the BJ potential, the BR potential, has been designed using the exchange hole in the hydrogen atom as a model. It has been shown to reproduce Slater’s averaged exchange potential and is, in general, a negative (attractive) potential. The second contribution, which is positive and proportional to √t/ρ, was introduced to correct the difference between the averaged exchange potential and the exact exchange potential, obtained by applying the optimized effective potential (OEP) method to the Hartree-Fock method. The BJ potential as the combination of these two parts is in excellent agreement with exact exchange OEP in atoms.
In Ref. 20, it has been shown that, in various types of solids, the BJ potential leads to only moderately improved band gaps compared to standard LDA and GGA.
The number of this parametrization is "4" and there is no file case.in0abp for this parametrization since this is a non empirical potential.
Socond parametrization: Modified version of Beck-Johnson of Tran-Blaha (P-Original )
However, in Ref. 21, a simple modification of the BJ potential (hereafter called TB-mBJ) was proposed,
The strength of the TB-mBJ exchange potential is that, as a multiplicative potential, it can predict band gaps of semiconductors and insulators with better accuracy than any other multiplicative potential and this at a computational cost of the order of a regular GGA calculation. It already has been used many times, and its performance has been analyzed in deep detail.22 This analysis showed that, although in many cases its performance was very good, there also are cases where it performs less satisfyingly (e.g., for itinerant metals or Cu2O).
The number of this parametrization is "1" and the file case.in0abp for this parametrization is as follows:
-0.012
1.023
0.5
Third parametrization: Parametrization of Koller ( P-Present)
The new parametrization for c is :
which has a more general form than Eq. (5).
However, They have observed that changing the value of the exponent e (from 0.2 to 1.5) only affects the quality of the fits a little, and thus, for simplicity, the exponent is fixed at e = 1.
The parameters A and B in Eq. (7) were then determined by minimizing the mean-absolute relative error (MARE) of a selection of the solids listed in Table I. First, all solids were used to optimize the parameters. This leads to parameters which are shown in Table II and, hereafter, are referred to as P-present. The calculation of the band gaps with the P-present parameters gives the results shown in Table I, which are compared with the band gaps obtained with the original TB-mBJ parameters and with the experimental results.
The number of this parametrization is "3" and the file case.in0abp for this parametrization is as follows:
0.488
0.500
1
Fourth parametrization: Parametrization of Semiconductors ( P-Semiconductor)
A parametrization made also by Koller
The P-present parameters are not optimal for the small-gap semiconductors, although they are better than original TBmBJ. Instead, They searched for new parameters which are optimal for the set of sp semiconductors, transition-metal oxides, and other transition-metal compounds.
The P-semiconductor parameters are better suited for the small-gap semiconductors.
The number of this parametrization is "2" and the file case.in0abp for this parametrization is as follows:
0.267
0.500
1
Summarization:
NB: For the parametrization of Beck-Johnson, there is no parameter to tune.
Reference: https://www.sfb-vicom.at/fileadmin/user_upload/proj_comp_mat_lab/0_vicom_publications_pdfs/Koller_et_al._-_2012_-_Improving_the_modified_Becke-Johnson_exchange_pote.pdf









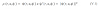

0 Comments