Hello,
I'm interested in checking the effect of pressure (uni-axial) on the band
structure. I first calculated the band structure with and without
spin-orbit interaction and was able to restore previous results.
Now, I want to see how the pressure affects the band structure. How can I
incorporate this into Wien2k?
The c over a optimization is the way to do it or I simply need to change
the lattice parameters of the initial structure?
Best regards,
Amit
Reply:
1- from Dr. Víctor Luaña
Amit,
1) Use thermodynamics
2) Your wien2k calculation is giving you the internal energy:
E = U(S,V), nominally at 0K, no zero temperature effect, and 0Pa.
3) To analyze pressure effects you can analyze the enthalpy or the
Gibbs funcion:
H(S,V) = U + pV
G(T,p) = U + pV -TS
If you have enough information on the vibrations of your system try
to study G, clearly. The zero temperature effect (ZPE, zero point
energy) has not been deeply studied in this field of solid state.
It is an interesting subject to explore better.
4) Look for papers in Phys Rev B on this subject. I have mine
available, so forgive me for citing mainly my publications on this
subject. The most recent are articles by Alberto Otero-de-la-Roza
and myself. For example:
Phys. Rev. B 84 (2011) 184103
5) On Computer Phys Commun you have freeware codes to do this task.
Look for the gibbs, asturfit and gibbs2 programs.
6) Notice that the codes in (5) are truly devoted to hydrostatic
conditions, no uni-axial situations. For that I would recommend
analyzing the grand potential
\Omegai(T,p,\vec{\mu}) = U +pV -TS - \vec{n} \vec{\mu}
(Sorry for the tex jargon)
If you want to analyze a pure substance, remember that
$\mu = g = G/n$, and \vec{n} = n.
Best regards,
Dr. Víctor Luaña
2- from Fecher gerhad
Hi Amit
You may calculate the single crystal elastic constants (sub-programs and
scripts are available in Wien2k) to find out how the lattice parameters change
under pressure.
If you apply pressure along some axis c, the remaining two axes a and b will
also change, usually become larger, only in few cases they may shrink also with
the pressure.
(Indeed, you can also check for changes in the lattice under shear or
combinations of different mechanical stress)
Might be good to have some exprimental data of the material to check if the
changes of the lattice under uniaxial pressure is correctly described.
If you have the new lattice parameters you can calculate the spaghetties as
usual.
Temperature is bad, it will force occupation of phonons that cause an energy
dissipation of the electrons.
This is , as far as I know, not implemented in Wien2k (maybe it is in some
Greens function codes that allow for complex potentials with an imaginary part
to simmulate the energy dissipation).
It will smear out the spaghettis.
Ciao
Gerhard







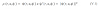
1 Comments
instruction of Gibbs2
ReplyDelete